In the last post, we looked at how records and ports work in DOT notation, and sketched out an API for incorporating them into Graphvix. In this post, we’ll dive deeper into the Elixir implementation.

This post is part of a series:

What we’ve covered

In the previous post, I wrote out a list of tasks necessary to incorporate records into Graphvix. Let’s revisit that list now and see what we’ve already handled

  1. create a Record struct, with an API to easily create rows and columns
  2. attach port names to cells in a Record struct
  3. generate correct DOT output for nodes with shape=record
  4. generate edge definitions using record ports

It looks like we finished tasks 1 and 2 in Part 7, so our next step is to take one of the Record structs we created and write code to correctly translate it into a DOT string representation.

Record into DOT

Let’s review the function signature of Graph.add_vertex/3:

def add_vertex(graph, label, attributes \\ [])

and the function signature of Record.new/2 is

def new(body, properties \\ [])

In order to convert a Record into a form that can be passed to add_vertex/3, we need to do two things:

  1. Generate the full label from the body attribute of the record node
  2. append [shape: “record] to the record node’s attributes

To make a clean API, let’s define Graph.add_record(graph, record), where the record argument is a Record struct. This function would be responsible for the two steps above, and passing those new values on to Graph.add_vertex/3:

def add_record(graph, %Record{body: body, attributes: attributes}) do
  label = Record.to_label(body)
  attributes = Keyword.put(attributes, :shape, "record")
  add_vertex(graph, label, attributes)
end

We’ve passed the responsibility of generating the label — the most involved part of this functionality — to the Record module, but this is in keeping with the Elixir mindset of keeping each function as simple and self-contained as possible.

Let’s turn our attention to label_from/1 in Record

def to_label(%{body: body}) when is_bitstring(body) do
  body
end
def to_label(%{body: subset = %RecordSubset{}}) do
  RecordSubset.to_label(subset, true)
end

The true we pass into the second definition of to_label is to let our function know that this first subset, whether a row or column, represents is the outer-most orientation in the record. This is important because at the top level, a row has no wrapping around it, while a column at the top level, or any nested row or column, is surrounded by { … }.

Once again, we have deferred functionality down another level, to the RecordSubset module. Again, we have two possibilities we need to handle. First, our subset is a row, and it is at the top level of the record. In that case, we need to generate a DOT string that is not surrounded by braces. Our second condition is any other case, in which case we want to ensure this subset is enclosed in the braces.

def to_label(subset, top_level \\ false)
def to_label(%{cells: cells, is_column: false}, _top_level = true) do
  Enum.map(cells, &_to_label/1) |> Enum.join(" | ")
end
def to_label(%{cells: cells}, _top_level) do
  [
    "{",
    Enum.map(cells, &_to_label/1) |> Enum.join(" | "),
    "}"
  ] |> Enum.join(" ")
end

Once again, deferment. Each cell of a subset can take one of three forms: it can be a string, a tuple represented a cell with a named port, or another subset. To handle these cases, we create the private method _to_label/1:

def _to_label(cell) when is_bitstring(cell), do: cell
def _to_label({port_name, cell}) do
  "<#{port_name}> #{cell}"
end
def _to_label(subset = %RecordSubset{}) do
  RecordSubset.to_label(subset)
end

If the cell is a string, the function needs only to return the string. If the cell has a named port, we interpolate the port name and the cell contents into the correct DOT notation. If the cell is a nested subset, we pass it back to the public function to_label/2, with the second argument (whether or not this subset is at the top level) defaulting to false.

An example

Before moving on to drawing edges to and from records and ports, let’s test out our new functions with a simple example. Using our sample from the end of the previous post, we now have the code written to generate a full DOT file out of it:

g = Graph.new()
{g, v1} = Graph.add_vertex(g, "normal node")
r = Record.new(["a", "b", Record.column([{"c_port", "c"}, "d"])])
{g, v2} = Graph.add_vertex(g, r)
Graph.to_dot(g)
"""
digraph G {

  v0 [label="normal node"]
  v1 [label="a | b | { <c_port> c | d }",shape="record"]

}
"""
Graph.write(g, "test.png")

The output of the final line of code gives us this image:

nodes.png

Edges

The final piece of this work, step 4 from the list at the top of the post, is to be able to generate edges that correctly connect records and ports.

As with add_vertex above, let’s review add_edge

def add_edge(graph, out_from, in_to, atttributes \\ [])

Right now out_from and in_to are the vertex ids generated by add_vertex. The simplest solution would be to pass, instead of a single id, a tuple of {vertex_id, port_name}. Let’s see what happens if we try to pass a tuple like that into :digraph.add_edge directly:

iex> digraph = :digraph.new()
iex> v0 = :digraph.add_vertex(digraph)
iex> v1 = :digraph.add_vertex(digraph)
iex> :digraph.add_edge(digraph, {v0, "port"}, v1)
{:error, {:bad_vertex, {[:"$v" | 0], "port"}}}

Uh oh! Looks like it’s not going to be that simple. What if we construct the full out_from value in correct DOT syntax and pass that in to add_edge?

iex> :digraph.add_edge(digraph, "v0:port", v1)
{:error, {:bad_vertex, "v0:port"}}

The same error! Indeed, looking at the :digraph documentation, it seems that our values for out_from and in_to need to be ids of vertices that already exist in the graph. So, how do we make sure ports, if they exist in the edge definition, are included in the final output?

The solution I came up with is to use the attributes Keyword list to temporarily store values I’ve named outport and inport. We’ll write a slightly modified version of add_edge that sets these values, and update the definition of edges_to_dot to check for, remove, and use these values if they exist. Let’s write some code!

def add_edge(graph, out_from, in_to, attributes \\ [])
def add_edge(graph, {id = [:"$v" | _], port}, in_to, attributes) do
  add_edge(graph, id, in_to, Keyword.put(attributes, :outport, port))
end
def add_edge(graph, out_from, {id = [:"$v" | _], port}, attributes) do
  add_edge(graph, out_from, id, Keyword.put(attributes, :inport, port))
end
def add_edge(graph, out_from, in_to, attributes) do
  eid = :digraph.add_edge(graph.digraph, out_from, in_to, attributes)
  {graph, eid}
end

With a function signature to show the default value for attributes, and our existing function definition at the bottom, this is the complete definition for add_edge. If one or the other of vertex arguments passed in is a tuple with a port name, the function will step through one (or both) of the first two definitions, each time passing the correctly modified values along until we reach the final definition.

Next, let’s look at how these values get used in edges_to_dot

defp edges_to_dot(graph) do
  [_, etab, _] = digraph_tables(graph)
  elements_to_dot(etab, fn edge = {_, [:"$v" | v1], [:"$v" | v2], attributes} ->
    case edge in edges_contained_in_subgraphs(graph) do
      true -> nil
      false ->
        v_out = edge_side_with_port(v1, Keyword.get(attributes, :outport))
        v_in = edge_side_with_port(v2, Keyword.get(attributes, :inport))
        attributes = attributes |> Keyword.delete(:outport) |> Keyword.delete(:inport)
        [
          "#{v_out} -> #{v_in}",
          attributes_to_dot(attributes)
        ] |> compact() |> Enum.join(" ") |> indent()
    end
  end)
end

defp edge_side_with_port(v_id, nil), do: "v#{v_id}"
defp edge_side_with_port(v_id, port), do: "v#{v_id}:#{port}"

elements_to_dot and edges_contained_in_subgraphs we have discussed in previous posts. The important code here is in the false branch of the case statement.

Using our helper method edge_side_with_port/2, we pass in the appropriate vertex id, and the result of looking in our attributes list for the correct port name, and have returned to us the correct syntax for that half of our edge definition, whether or not there is a port name attached.

Then we delete those two keys and their values, if they exist, from the attributes list, to ensure they do not appear in the printed out list of DOT attributes associated with the edge.

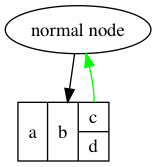
Let’s revisit our example from above, and include a couple edges to show this new code working as we expect it to:

g = Graph.new()
{g, v1} = Graph.add_vertex(g, "normal node")
r = Record.new(["a", "b", Record.column([{"c_port", "c"}, "d"])])
{g, v2} = Graph.add_vertex(g, r)
Graph.to_dot(g)
{g, _e1} = Graph.add_edge(g, v1, v2)
{g, _e2} = Graph.add_edge(g, {v2, "c_port"}, v1, color: "green")
"""
digraph G {

  v0 [label="normal node"]
  v1 [label="a | b | { <c_port> c | d }",shape="record"]

  v0 -> v1
  v1:c_port -> v0 [color="green"]

}
"""
Graph.write(g, "test.png")

edges.png

And voila! We can see the green edge pointing out from the “c” cell of our record.

The code up until this point is tagged here: GitHub - mikowitz/graphvix at v1.0.0.pre.records

Between this and the previous post, we’ve covered a lot of ground, both conceptually and in code. There is one final piece of Graphvix to write that lets us manipulate the final layout of a graph, aligning related vertices and subgraphs to create timelines, defined hierarchical structures, etc. That is the concept of rank, which we’ll be exploring in our next, and probably final, post in this series. Thanks for reading this far, and I’ll see you back here for the next post.